
 |
Eager Space | Videos by Alpha | Videos by Date | All Video Text | Support | Community | About |
|---|


nd that's why starting a launch company is a bad decision...

Spaceplanes are great.
Who wouldn't want to start on the ground and take a single vehicle all the way into orbit?

The media has written many articles about spaceplanes and how great they will be.

And yet, none of the spaceplane designs have made it to actual hardware, though a design without wings did:
(show video)
The DC-X demonstrators made 12 flights in the 1990s. The highest flight reached 3 kilometers in altitude, but an explosion after landing on the 12th flight led to the cancellation of the program.
Where are the spaceplanes?
This is...

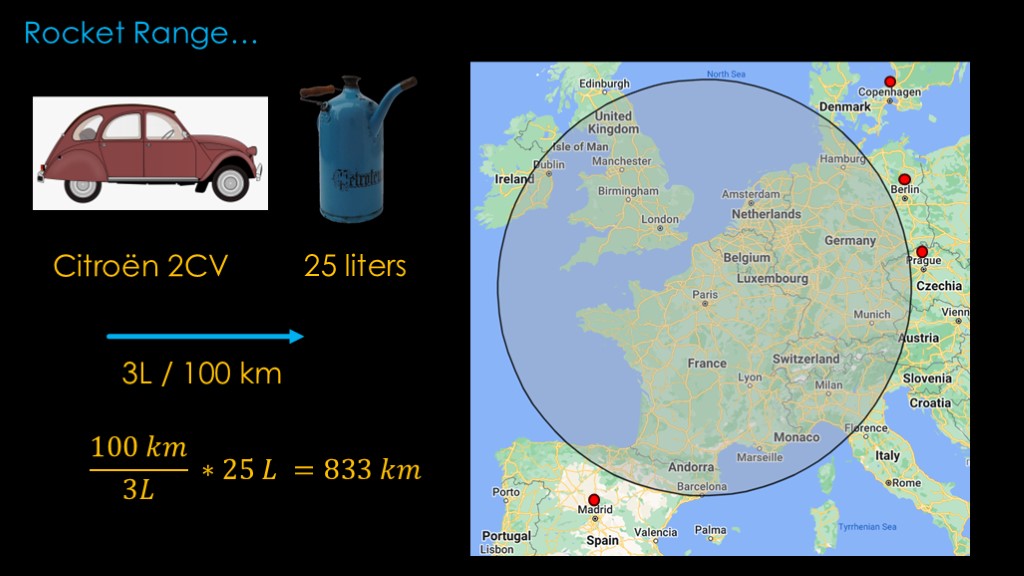
To understand why there aren't any single stage spaceplanes, we need to understand how fuel capacity, payload, and range work for rockets.
For cars it's pretty easy...
The Citroen 2CV requires 3 liters of gas to travel 100 kilometers.
It has a fuel tank that holds 25 liters, and a little bit of math tells us that it can travel 833 kilometers on one tank of gas.
That's an impressive range that covers all of France, the Netherlands, and Switzerland, but you can't get to Copenhagen, Berlin, Prague, or Madrid.
That's carrying only a driver. If we were carrying more payload - 3 passengers for example - our mass would go up and our range would go down.

For space, we don't use kilometers as a measure of distance; we use a measurement known as "delta v", which is measured in meters per second. Sometimes we write it using the lowercase greek letter "delta".
To get from the surface into low earth orbit requires around 9400 meters per second of delta v - that's the distance we need to cross.
Like a car, a specific rocket has a delta-v capability that varies based on the amount of payload it is carrying. This Soyuz FG rocket can carry 6,900 kilograms to low earth orbit.

If you want to know more about delta v distances in the solar system, see my video "planning your solar system road trip".

At this point to talk about the physics of rocketry.
I'll be doing all the math and the physics will not be on the test, so just pay attention to the basic concepts.
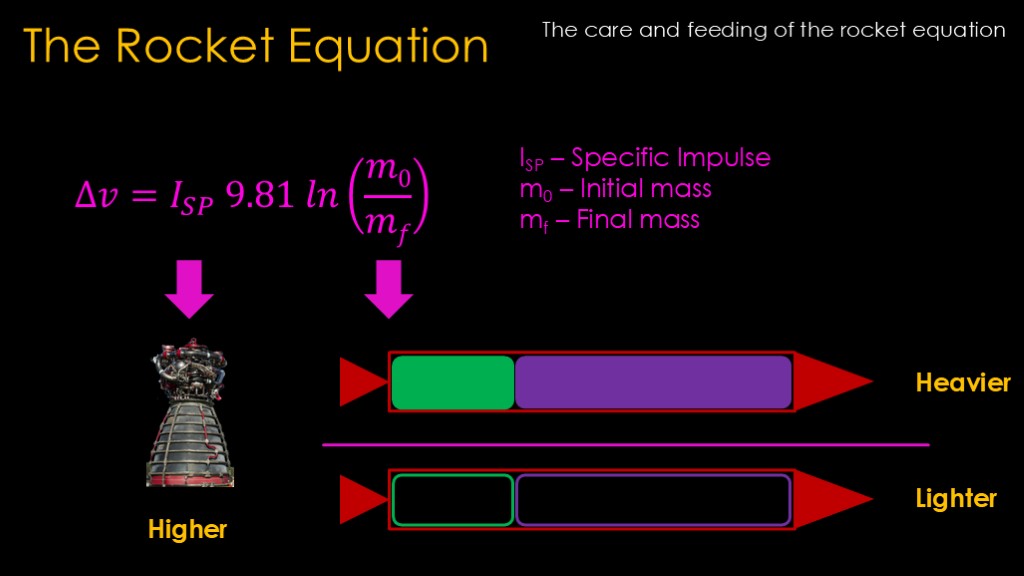
It is possible to estimate the amount of delta v that a rocket can generate using the rocket equation.
If you want all the details of the rocket equation, go watch my video titled "the care and feeding of the rocket equation". Here are highlights.
The first term of the equation is the specific impulse, often written as ISP. The specific impulse depends on the design of the engine and the propellants that it uses. A higher value is better as that results in a higher delta v - the rocket can travel farther on a given amount of fuel. Its like the fuel economy of a car.
The second term is known as the mass ratio and has two parts. We take the initial mass when the rocket is fully loaded with propellant and we divide that by the final mass when all the propellant is gone. The ln term is the natural logarithm, which is there because physics.
We want the mass ratio to be as high as possible, which mean carrying as much propellant as possible and making the empty stage as light as possible.
Higher payload increases both the initial mass and the final mass, reducing the mass ratio and resulting in less delta v. Like our car, if we have a heavier load we can't go as far.

It's common to find people asking whether a specific rocket stage can make it into orbit as a single stage. Let's look at the Falcon 9.
Note that all the numbers I'll be using are estimates and I'm ignoring some other factors, so the conclusions we reach are for entertainment purposes only.
The specific impulse of the merlin engines used on the first stage is 297.
The final mass is the mass of the empty stage, which is 27,200 kilograms.
The initial mass is the final mass plus the mass of propellant, giving a total of 445,900 kilograms.
Plug that into the rocket equation, do the math, and we end up with the number 8,150 meters per second of delta v. That does not reach the threshold to get into orbit, so this stage cannot operate as a single stage to orbit vehicle.
It's tempting to look that delta v number and say, "8150 is pretty close to 9400 so we should be able to get there". This is not the case - this stage would need to add 60% more propellant or reduce the final mass by 60% to get to 9400 meters per second. That's just not possible.
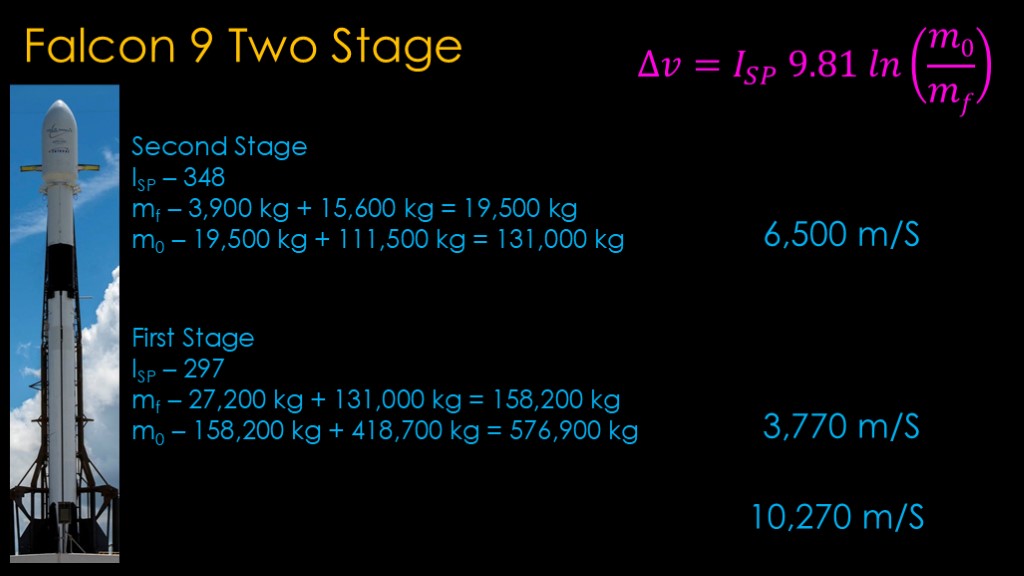
Looking at the two-stage version, we can use the second stage numbers with it carrying a payload of 15,600 kilograms and determine that the second stage can generate 6,500 meters per second of delta v.
The first stage carries the fully-fueled second stage as a payload, and when we run the numbers we find that it can generate 3,770 meters per second of delta v, for a total of 10,270 meters per second of delta v. That's enough to get into orbit plus leave enough extra for the first stage to return to earth and land on a drone ship.
Our single-stage version couldn't get into orbit at all, and our two-stage version can carry over 15 tons into orbit.

That's why orbital rockets pretty universally use at least two stages.

But the point of this video is to talk about spaceplanes, so we'll need to define the problem in more detail.
If we are going to build a single stage to orbit rocket, we will need to somehow squeeze 9400 meters per second of delta v out of it.
We can plug that into the rocket equation, and then solve for the mass fraction, and we get this equation because math. E is a numerical constant equal to about 2.72 and shows up as the inverse of the natural log. Note that the mass fraction depends on the specific impulse.
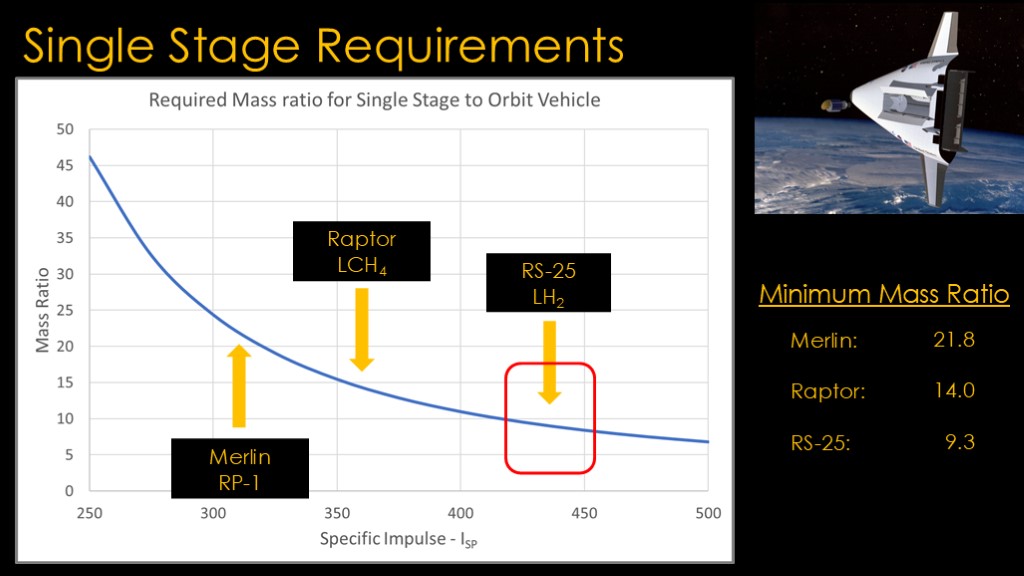
Using that equation, we can come up with a graph that tells us what mass ratio we need to achieve for a given specific impulse.
The higher the specific impulse, the lower the mass ratio required to get the delta V we need to get into orbit.
We can add some sample engines here.
The SpaceX Merlin used on Falcon 9 burns RP-1 fuel, and has a specific impulse of 311. That translates to a required mass ratio of 21.8.
The SpaceX Raptor used on Starship burns liquid methane fuel and has a specific impulse of 363 and requires a mass ratio of 14.
The RS-25 used on the Space shuttle and SLS has a specific impulse of 431 and requires a ratio of only 9.3.
The high specific impulse of liquid hydrogen appears to be the obvious choice for a single stage to orbit design. To explore further we need more specifics, and that means we need a rocket...

We can use the SLS Core Stage as an example, as it conveniently uses 4 RS-25 engines.
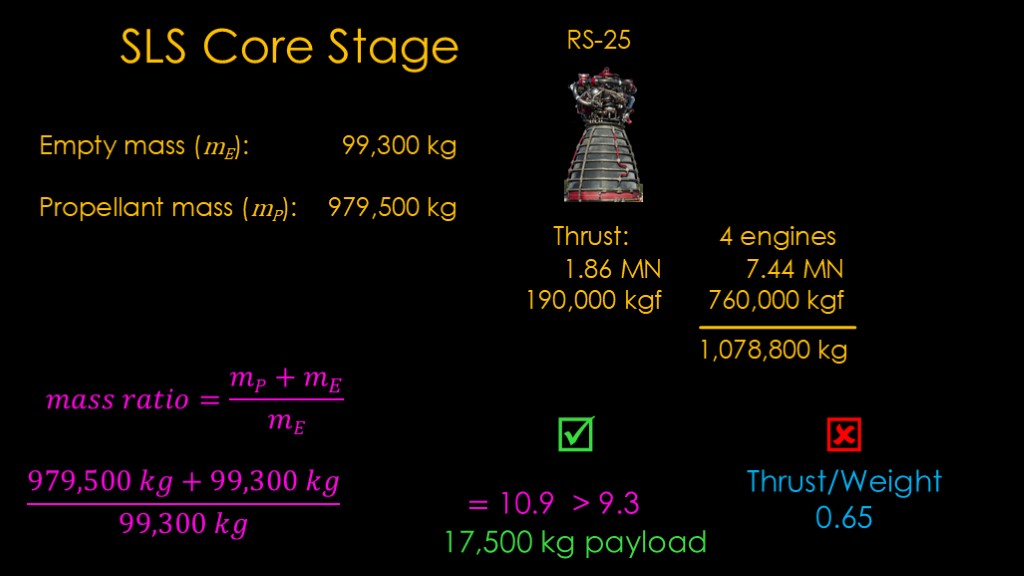
The information we need to know about the SLS core stage is published but it's a little squishy. These are the best numbers I could find.
The empty mass of the stage is 99,300 kilograms.
The stage holds 979,500 kilograms of propellant.
We can compute the mass ratio using the following equation.
Plug the numbers in, and we get 10.9. Our threshold for this fuel and engine choice was 9.3, so this scenario gets a big green checkmark as the mass ratio is high enough to get us into orbit. We can do a few more calculations and figure out that we could carry 17,500 kilograms of payload.
This looks great...
But it turns out that we forget something...
The RS-25 engine creates a thrust of 1.86 Meganewtons at sea level. Newtons is the proper unit of force in the metric system, but for our use kilograms of force is more convenient, so a quick bit of math shows that this is 190,000 kilograms of force.
There are 4 engines on the core stage, so the total is 7.44 meganewtons or 760,000 kilogram of force.
We know from our earlier numbers that the total mass is 1,078,800 kilograms, so we can do a quick division and and we find the thrust to weight ratio at launch is 0.65.
It turns out that our single stage to orbit rocket lacks the thrust to get off the pad.
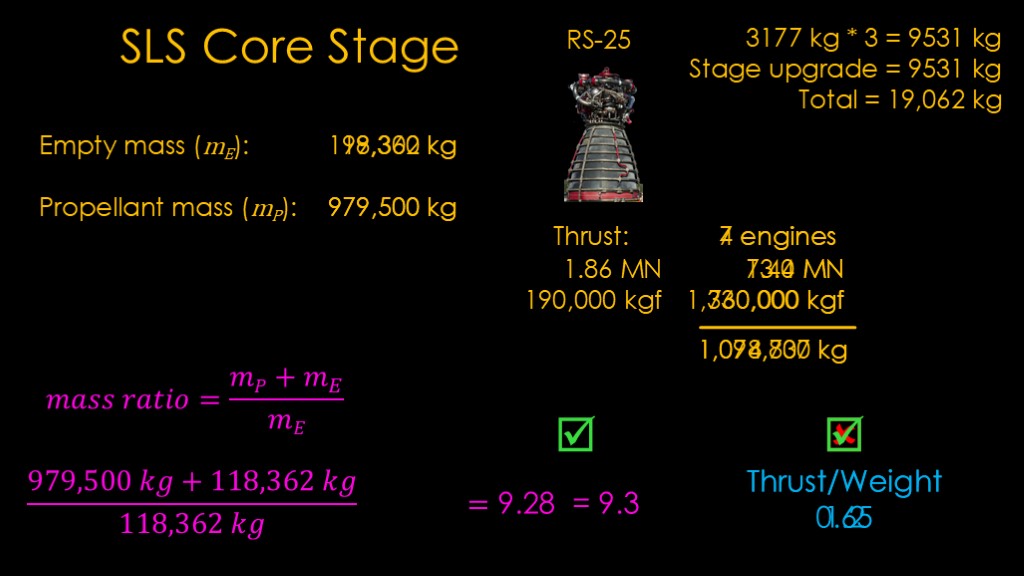
What we need is more engines. Seven engines pushes the thrust up to a little over 1.3 million kilograms which looks like it's in the right ballpark.
There is a downside - each of these new engines adds about 3177 kilograms in mass, for a total of 9531 kilograms. We also need to make the stage bigger to hold those new engines, so I'm going to arbitrarily assume that changes to the stage to support the additional engines costs the same mass, so our total mass increase is 19,062 kilograms. That increases our empty mass.
Run the numbers again, and we find that our mass ratio is reduced to 9.28. Our thrust to weight is 1.2, so that's good.
At this point we have a marginal single stage to orbit vehicle. We can probably get it into orbit but without any payload.

Note that so far we've just been talking about an empty stage, but if we are building a spaceplane, we need to add in wings, landing gear, and some sort of thermal protection system.
I wasn't able to find any proposal that gives overall vehicle masses so it's hard to know how much it would add. The space shuttle orbiter was made of aluminum and massed about 78,000 kilograms and it was considerably smaller than the stage we are considering here. Titanium would be lighter if you could afford to use it; carbon fiber could be very light but would make the thermal protection system heavier.

There's a problem with developing single-stage-to-orbit vehicles, and that's the impact of increases in mass.
Let's say that our target mass was 90,000 kilograms for the vehicle and a 10,000 kilogram payload.
But it turns out that our estimates were low, and our stage is 5% heavier. Every kilogram of extra mass in the vehicle is one less kilogram of payload, and that 5% increase nearly cuts our payload in half.
If we're running a two-stage rocket and our second stage gets 5% heavier, we only lose a small amount of payload because the second stage doesn't have a lot of mass. Most of the mass is in the first stage.
If the first stage gets heavier, it doesn't matter than much because the first stage does not go into orbit; in our scenario here a 1360 kilogram increase in empty mass only results in a payload reduction of 200 kilograms - it takes an extra 6 kilograms in the empty mass of the first stage to reduce the payload by 1 kilogram.
Keeping the single stage to orbit vehicle light is absolutely critical, as 10% mass gain could eliminate all the payload. That means expensive materials and expensive development, and even with that it's not sure that the vehicle will have meaningful payload when it's finished. That makes it a risky investment.
It's much less important for two-stage vehicles. There isn't much mass in the upper stage so growth there doesn't matter much, and mass growth in the lower stage isn't very important either. Extra mass matters but it's unlikely to be enough to kill the program.
Are there any ways we can cheat and improve this situation? The answer is yes...

What we need is more engines. Two extra engines is marginal, but if we add 3 engines, that pushes the thrust up to a little over 1.3 million kilograms which looks like it's in the right ballpark.
There is a downside - each of these new engines adds about 3177 kilograms in mass, for a total of 9531 kilograms. We also need to make the stage bigger to hold those new engines, so I'm going to arbitrarily assume that changes to the stage to support the additional engines costs the same mass, so our total mass increase is 19,062 kilograms. That increases our empty mass.
Run the numbers again, and we find that our mass ratio is reduced to 9.28. Our thrust to weight is 1.2, so that's good.
At this point we have a marginal single stage to orbit vehicle. We can probably get it into orbit but without any payload.

The Falcon 9 uses subchilled propellants that have a higher density so they can stuff more propellant in a given stage and therefore improve our mass ratio.
We can do that with our stage - we can subchill the liquid hydrogen and liquid oxygen so that they are approximately 8% denser, and that will allow us to put more propellant in our tanks, and that will improve our mass ratio.
If we can get 8% increase in density for both the liquid hydrogen and oxygen, we would theoretically get 9,500 kilograms of payload increase. However, the increased liftoff mass will either require an 8th engine that makes the stage heavier or will result in increased gravity losses that will consume some of that payload increase. It's worth doing but it does have some side effects.
That is assuming that it's practical to use subchilled hydrogen. NASA has done some research but normal liquid hydrogen is already very challenging to deal with and nobody has built a rocket or engine that uses subchilled hydrogen.
If it's only possible to subchill the oxygen, the increase in payload is much smaller, only 3000 kilograms.

Radian Aerospace has an interesting idea.
Rather than launch the spaceplane from a runway, you can put it on a rocket-powered sled that accelerates it to approximately 200 meters per second before releasing the plane.
That by itself reduces the required mass ratio from 9.3 to 8.8.
That will make the spaceplane much easier to build, but the rocket sled limits your launch locations, requires more complexity during the development process, and failures during the rocket sled run could be problematic.

Reaction engines has an engine concept known as SABRE that they are hoping to use in their Skylon spaceplane.
SABRE is a hybrid engine. At low altitude it functions like a jet engine, burning liquid hydrogen with oxygen pulled out of the air, and in vacuum, it burns liquid hydrogen and liquid oxygen.
It's an interesting concept...
Being able to burn atmospheric oxygen provides a great advantage at lower altitude and results in a very high specific impulse.
But the hybrid engine is going to be much heavier than a conventional rocket, and the atmospheric oxygen content drops off quickly as you go higher, so the weight penalty will hurt the mass ratio when in rocket mode.
It's also a complex system, having to deal with hypersonic airflow, liquid hydrogen, liquid oxygen, and a complicated engine system.
Of the cheats, subchilled propellants are useful and sled launch and SABRE are maybe practical, maybe not.

I'm sure somebody is wondering about starship. It's already equipped to come back and land, so can we operate it in single stage to orbit mode?
Because the Raptor engine burns liquid methane, it has a considerably lower specific impulse than the RS-25, so that means Starship will need a much higher mass ratio, all the way up at 14. That seems like a significant disadvantage - we chose the RS-25 because the high specific impulse meant it required the lowest mass ratio.
But there's more going on here. The starship tanks are only about half the length of the SLS core stage tanks and are roughly half the volume.
Despite that, starship manages to stuff 20% more propellant mass into its tiny tanks than SLS can stuff into its tanks.
The problem is the low density of liquid hydrogen. The low density of hydrogen is one of the main factors that results in a higher specific impulse but that low density also means that the SLS tanks are roughly 2.3 times the size of the starship ones, which makes the empty stage heavier and reduces the mass fraction. If we look at the propellant density we see that it is much higher in starship.
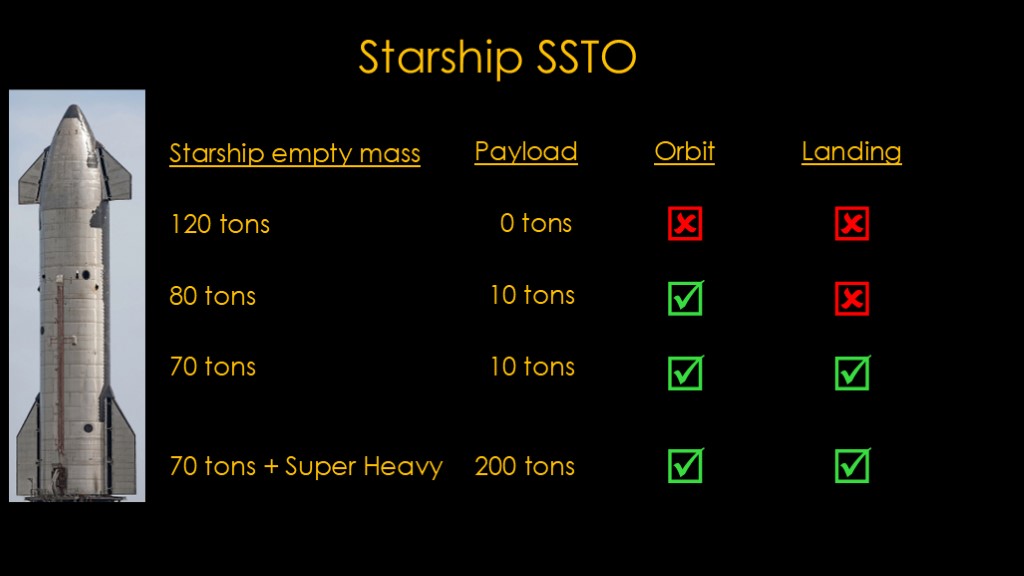
That's not the question you wanted an answer to, but unfortunately starship is still in development and we don't have good numbers for the mass of the production version or even the current test version, so I can't give a yes/no answer to whether it can make it to orbit.
But I can talk about a few scenarios...
Based on the amount of propellant I used on the last slide, if the starship empty mass is 120 tons and there is no payload, it can't get into orbit or land.
If its mass is 80 tons, it can get into orbit with a 10 ton payload but will not have enough fuel to reenter and land, and if it has a mass of 70 tons, it can carry 10 tons into orbit and return to land.
So if it gets light enough, it can sorta maybe function as a single stage to orbit vehicle. That 70 tons seems quite low, but SpaceX has talked about stretching starship to make it taller so it could carry more fuel, and that would improve the mass ratio.
However, if starship is light enough to carry 10 tons into orbit by itself, it will be able to do around 200 tons when launched by super heavy so the SSTO version doesn't seem very exciting IMO.

Why don't we have spaceplanes?
It's pretty simple... It's because physics hates humans.
It's hard enough to build a two-stage rocket that can make it into orbit when you play on normal mode, but trying to build a single stage vehicle that can land back on earth is playing on legendary.
It's just too hard to do and has become even less interesting with SpaceX showing how to reuse the first stage of a rocket.

If you enjoyed this video, please join the movement to repeal the rocket equation